MASA

De -
¿Que es la masa?
Resultado de imagen para que es la masa en fisica
Como masa designamos la magnitud física con que medimos la cantidad de materia que contiene un cuerpo. Como tal, su unidad, según el Sistema Internacional de Unidades, es el kilogramo (kg).La masa de un cuerpo es una propiedad característica del mismo, que está relacionada con el número y clase de las partículas que lo forman. Se mide en kilogramos (kg) y también en gramos, toneladas, libras, onzas, etc. El peso de un cuerpo es la fuerza con que lo atrae la Tierra y depende de la masa del mismo






MASA Y PESO 


Calcular la masa de un cuerpo que al recibir una fuerza de 20 N adquiere una aceleración de 5 m/s².
De la ecuación dada despejamos la masa "m":
m = F/a
Reemplazamos y calculamos:
m = 20 N/(5 m/s²)                                                           Datos:   F = 20 N       a = 5 m/s²
Recordando que 1 N es 1 kg.m/s²:
m = 4 (kg.m/s²)/(5 m/s²)                                                   Fórmulas:
                                                                                                   F = m.
m = 4 kg



FUERZA E INTERACCIONES.
En el lenguaje cotidiano, fuerza es un empujón o un tirón. Una mejor definición es que una fuerza es una interacción entre dos cuerpos o entre un cuerpo y su ambiente. Es la causa de por qué siempre nos referimos a la fuerza que un cuerpo ejerce sobre un segundo cuerpo. Estas son las causas del movimiento. Por ejemplo, ¿cómo puede ser un remolcador empujar un trasatlántico que es muchísimo pesado que él? ¿Por qué es más difícil controlar un automóvil en el hielo en concreto seco? Las respuestas a estas preguntas ya otros nos han llevado tema de la dinámica, es decir, la relación entre el movimiento y las fuerzas que lo causan.

En los vínculos que conforman esta sección de estudio explicaciones claras sobre el concepto general de Fuerza, Leyes de Newton, Descomposición de Fuerzas; y esta compuesta por tres ítems: Fuerza, Trabajo y Energía.


Resultado de imagen para FUERZAS E INTERACCIONES







¿Cuál será la aceleración del sistema y la tensión de la cuerda suponiendo que hay movimiento y que m1 = 5 kg y m2 = 2 kg y µd vale 0,08?

Cuerpo 1: Cuerpo 1: T – Frd = m1 · a ⇒ T – µd · m1 · g = m1 · a 
Cuerpo 2: Cuerpo 2: P2 – T = m2 · a ⇒ m2 · g – T = m2 · a 
2 kg · 9,8 m/s2 – 0,08 · 5 kg · 9,8 m/s2 = (5 kg + 2 kg) · a 
2 kg · 9,8 m/s2 – 0,08 · 5 kg · 9,8 m/s2 a 
= 2,24 m/s 2,24 m/s2 5 kg + 2 kg T =
 5 kg · 2,24 m/s2 + 0,08 · 5 kg · 9,8 m/s2 = 15,12 N




ENERGÍA MECÁNICA 
La rama de la física que estudia y analiza el movimiento y reposo de los cuerpos, y su evolución en el tiempo, bajo la acción de fuerzas se denomina mecánica. En un cuerpo existen fundamentalmente dos tipos de energía que pueden influir en su estado de reposo o movimiento: la energía cinética y la potencial.


Resultado de imagen para energia mecanica





CONDICIÓN DE EQUILIBRIO 
Las condiciones de equilibrio son las leyes que rigen la estática. La estática es la ciencia que estudia las fuerzas que se aplican a un cuerpo para describir un sistema en equilibrio. Diremos que un sistema está en equilibrio cuando los cuerpos que lo forman están en reposo, es decir, sin movimiento. Las fuerzas que se aplican sobre un cuerpo pueden ser de tres formas:
-Fuerzas angulares: Dos fuerzas se dice que son angulares, cuando actúan sobre un mismo punto formando un ángulo.

Fuerzas colineales: Dos fuerzas son colineales cuando la recta de acción es la misma, aunque las fuerzas pueden estar en la misma dirección o en direcciones opuestas.

-Fuerzas paralelas: Dos fuerzas son paralelas cuando sus direcciones son paralelas, es decir, las rectas de acción son paralelas, pudiendo también aplicarse en la misma dirección o en sentido contrario.

 Resultado de imagen para condiciones de equilibrio






Dos cables sostienen un semáforo cuyo peso tiene una magnitud de 240 N, formando un ángulo de 150° con ambas cuerdas, tal como se muestra en la figura. Calcule la magnitud de la fuerza aplicada por cada cable. 
Solución:
Elaboramos el diagrama de cuerpo libre de nuestro problema, extrayendo primero las fuerzas que están activas en dicho cuerpo, incluyendo los ángulos.
                                         
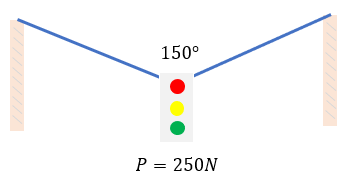
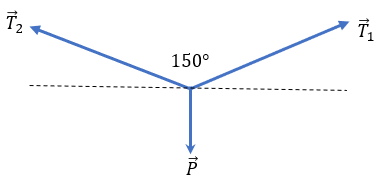
Como los cables están generando una tensión con los postes que soportan al semáforo, van en dirección a los postes, no al semáforo. El peso del semáforo hace que la fuerza jale hacía abajo. Una vez teniendo en cuenta dicho punto, es momento de realizar un diagrama de cuerpo libre más completo, colocando las fuerzas en el plano cartesiano.
Hemos colocado 15° en los ángulos de las tensiones con la horizontal, ya que el ángulo que había entre cable y cable eran de 150°. Es lógico que los ángulos restantes fueran 30°, ahora vamos a colocar la sumatoria de fuerzas en el eje “x”
\displaystyle \sum{{{{\vec{F}}}_{x}}}=0
Observamos por nuestro plano cartesiano, que solamente lo que está de lado derecho es positivo, y de lado izquierdo negativo.
Para el eje “x”
\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{\overrightarrow{T}}_{1}}_{x}-{{\overrightarrow{T}}_{2}}_{x}=0
Para el eje “y”
\displaystyle \sum{{{\overrightarrow{F}}_{y}}}={{\overrightarrow{T}}_{1}}_{y}+{{\overrightarrow{T}}_{2}}_{y}-P=0
Resolviendo para el eje “x”
Como bien sabemos, tenemos que descomponer nuestros vectores en su forma rectangular de tal forma que:
\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{T}_{1}}\cos 15{}^\circ -{{T}_{2}}\cos 15{}^\circ =0
Al tratarse de una igualdad, vamos a despejar de tal forma que nos quede así:
\displaystyle {{T}_{1}}\cos 15{}^\circ ={{T}_{2}}\cos 15{}^\circ
\displaystyle {{T}_{1}}={{T}_{2}}
Esto nos da entender, que tanto la tensión 1 como la tensión 2, son iguales. Ahora lo que necesitamos saber es cuanto vale la tensión, y ese dato nos arrojará cuando resolvamos para el eje “y”.
Resolviendo para el eje “y”
\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ -250N=0
\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ =250N
Pero como sabemos que:
\displaystyle {{T}_{1}}={{T}_{2}}
\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{1}}sen15{}^\circ =250N
Es decir:
\displaystyle 2{{T}_{1}}sen15{}^\circ =250N
Despejando a T1
\displaystyle {{T}_{1}}=\frac{250N}{2sen15{}^\circ }=482.96N
Esto quiere decir que tanto T1 como T2 tienen una fuerza de tensión de 482.96 Newtons cada una.
Resultado:
\displaystyle {{T}_{1}}={{T}_{2}}=482.96N

FUERZA GRAVITACIONAL 

Sir Isaac Newton, durante su retiro en una granja de Woolsthorpe durante los años 1665-1666 elaboró la base de lo que hoy se conoce como la ley de gravitación universal, basándose en las leyes de Kepler sobre el movimiento de los planetas y los estudios de Galileo.


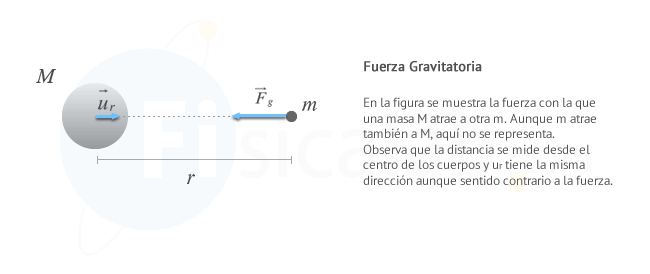
Esta ley establece que los cuerpos, por el simple hecho de tener masa, experimentan una fuerza de atracción hacia otros cuerpos con masa, denominada fuerza gravitatoria o fuerza gravitacional. Esta fuerza, explica entre otras muchas cosas, por qué orbitan los planetas.
La fuerza gravitacional entre dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. Matemáticamente se expresa de la siguiente forma:
F→g=−G⋅M⋅mr2⋅u→r
donde:
  • G es la constante de gravitación universal, G = 6,67·10-11 N·m2/kg2
  • M y m son las masas de los cuepos que interaccionan
  • r es la distancia que los separa.
  • u→r es un vector unitario que expresa la dirección de actuación de la fuerza.
De igual forma, el módulo de dicha fuerza se puede obtener mediante la siguiente ecuación:
Fg=G⋅M⋅mr2
En la figura se muestra la fuerza con la que una masa M atrae a otra m. Aunque m atrae también a M, aquí no se representa. Observa que la distancia se mide desde el centro de los cuerpos y ur tiene la misma dirección aunque sentido contrario a la fuerza.














Comentarios

Publicar un comentario

Entradas populares de este blog

MOVIMIENTO CIRCULAR UNIFORME ACELERADO

De -
Imagen
El  movimiento circular uniformemente acelerado (MCUA)  se presenta cuando una partícula o cuerpo sólido describe una  trayectoria  circular aumentando o disminuyendo la velocidad de forma constante en cada unidad de tiempo. Es decir, la partícula se mueve con aceleración constante. En el dibujo se observa un ejemplo en donde la  velocidad aumenta  lineal mente  en el tiempo. Suponiendo que el tiempo en llegar del punto P 1  a P 2  sea una unidad de tiempo, la partícula viaja con una  aceleración tangencial  uniforme  v , incrementándose esa cantidad en cada unidad de tiempo. Una bola de 0,5 kg. De masa esta unida al extremo de una cuerda cuya longitud es 1,5 metros. La figura 6.2  muestra  como gira la bola en un círculo horizontal. Si la cuerda puede soportar una tensión máxima de 50  Newton , Cual es la velocidad máxima que la bola puede alcanzar antes de que la cuerda se rompa? Solución:...
Leer más